kontakt

Skąd te liczby?

• Liczby naturalne
• Liczby wymierne
• Liczby całkowite
• Liczby niewymierne

Co to jest liczba? Co to jest liczba trzy lub co to jest liczba pięć? Ktoś powie, że liczba jest to ilość elementów w jakimś zbiorze, np. trzy kwiaty w wazonie, pięciu uczniów w klasie. Niezbyt to precyzyjna definicja ale na początek może być. Liczby jeden, dwa, trzy ...(każda o jeden większa od poprzedniej) są liczbami naturalnymi i mówimy, że są "abstrakcją wyników procesów liczenia przedmiotów w zbiorach skończonych". Oznacza to, że wszystkie zbiory, które mają tyle samo elementów określają jedną liczbę naturalną. Ludzie próbowali liczyć od bardzo dawna. Ale potrzeba było wieków, aby odkryć, że para koni i dwa dni określają tę samą liczbę dwa.

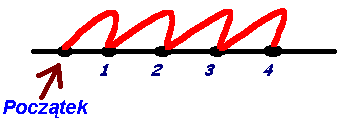
Liczby naturalne można przedstawić na osi liczbowej. Początek osi nazywamy liczbą zero. Istnienie liczby zero nie zawsze było oczywiste. Choć liczby naturalne znane były w czasach starożytnych, to zero pojawiło się dopiero u Hindusów prawdopodobnie ok. 600 r. n. e. Od Hindusów przejęli ją Arabowie a od Arabów kultura matematyczna dotarła do Europy. Był to wiek X. W Europie używane były wtedy cyfry rzymskie lub słowne określenia liczb i potrzeba było aż pięciu wieków, żeby ten system liczenia został wyparty przez system arabski. System ten używany jest do dziś. Aby zobrazować liczbę dziesięć piszemy 10, liczbę piętnaście zapisujemy jako 15. Poszczególne pozycje cyfry w liczbie, patrząc od prawej strony, oznaczają jedności, dziesiątki, setki itd. Krótko mówiąc posługujemy się dziesiątkowym systemem pozycyjnym. Dziesiątkowy system nie jest jedynym systemem pozycyjnym. Liczby można przedstawić w systemie o dowolnej podstawie.

To nie jest samochód, to rysunek samochodu!	7 to symbol którym określamy liczbę siedem!

Możemy mówić o zbiorze liczb naturalnych. Zbiór ten oznaczamy literą N. N={1, 2, 3, ...}. Zawsze w tym miejscu jest kłopot z zerem. Zero jest czy nie jest liczbą naturalną? Najgorzej, że sami matematycy nie są w tym miejscu zgodni. My umówimy się, że zero nie należy do N
W zbiorze liczb naturalnych wprowadzono działania dodawania i mnożenia. Przypomnijmy sobie co wiemy o zbiorze N z działaniami dodawania i mnożenia.

1. Dodawanie jest przemienne, to znaczy, że dla dowolnych liczb naturalnych n, m n+m daje dokładnie taką samą liczbę co m+n tj. n+m=m+n.
   
2. Dodawanie jest łączne, to znaczy (n+m)+p=n+(m+p).
   
3. Mnożenie jest przemienne: mn=nm.
   
4. Mnożenie jest łączne: (mn)p=m(np).
   
5. Mnożenie jest rozdzielne względem dodawania: m(n+p)=(mn)+(mp).
   
6. W zbiorze liczb naturalnych jest liczba najmniejsza - jest nią 1, ale nie ma liczby największej.
   
7. W zbiorze liczb naturalnych każda następna liczba jest większa od poprzedniej o jeden.
   
8. Między dwiema kolejnymi liczbami naturalnymi nie ma żadnej innej liczby naturalnej.

Mówiąc o własnościach liczb naturalnych nie posługiwaliśmy się zapisem liczby w systemie pozycyjnym, ani w ogóle żadnym zapisem liczby. Własności te są własnościami liczb i nie zależą od zapisu liczby.
Pitagoras - V w. p.n.e. - znał następującą własność liczb: suma pewnej ilości kolejnych liczb nieparzystych od jedynki począwszy, jest kwadratem jakiejś liczby naturalnej:
1=1²
1+3=2²
1+3+5=3²
1+3+5+7=4²
Pitagoras jednak nie zapisywał tego tak jak my. Grecy nie znali systemu pozycyjnego, używali literowego systemu liczbowego. Dowód Pitagorasa wyglądał następująco:

Liczby naturalne powstały na skutek liczenia pojedynczych przedmiotów. W życiu codziennym nie tylko jednak liczymy, również mierzymy różne wielkości, np. długość, pole powierzchni, masę, ciężar, itd. W każdym przypadku mamy jakąś jednostkę i liczymy, ile tych jednostek ma mierzona wielkość. Prawie zawsze mierzona wielkość zawarta jest pomiędzy kolejnymi wielokrotnościami obranej jednostki (między dwiema sąsiednimi liczbami naturalnymi). W takich sytuacjach przyjętą jednostkę dzielimy na pewną ilość mniejszych jednostek, np. połowę poprzedniej, trzecią część poprzedniej, jej dziesiątą część, itd. Tę nową jednostkę oznaczamy symbolem 1/n, gdzie n jest liczbą podziału jednostki wyjściowej. Jeśli mierzona wielkość posiada m nowych jednostek, to zapisujemy tę miarę m/n. Symbol ten nazywamy ułamkiem. Ułamek m/n jest zapisem liczby, którą nazywamy wymierną.

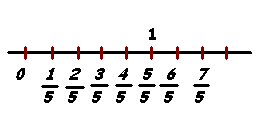
Liczba wymierna, jako liczba, ma swoje miejsce na osi liczbowej. Jeśli odcinek jednostkowy podzielić na n równych części, to punkty podziału przedstawiają ułamki o mianowniki n.

Jak między dwiema sąsiednimi liczbami naturalnymi nie można znaleźć trzeciej, tak w przypadku liczb wymiernych nie można nawet stwierdzić, które z nich są sąsiednie. Pomiędzy każdymi dwoma liczbami wymiernymi istnieją inne liczby wymierne.
Każdą liczbę wymierną można przedstawić przez nieskończenie wiele ułamków: np. 1/2, 2/4, 5/10 - wszystkie te ułamki określają jedną liczbę wymierną, w tym przypadku połowę całości. Najchętniej jednak posługujemy się najprostszymi ułamkami, np. 1/2, 3/5. W ułamkach nieskracalnych liczby naturalne przedstawiające licznik i mianownik nie mają wspólnej miary poza jednością. O takich ułamkach mówimy, że są względnie pierwsze.

Zajmijmy się znowu osią liczbową. Odkładając jednostkę na prawo zaznaczamy kolejne liczby naturalne. Gdy zrobimy to samo na lewo od zera to otrzymamy wtedy przedstawienie na osi liczb ujemnych całkowitych. Zero jest liczbą całkowitą.Zbiór liczb całkowitych oznaczamy: Z={...,-3, -2, -1, 0, 1, 2, 3, ...}. Liczby całkowite można dodawać, mnożyć, odejmować, czasami dzielić

Najwięcej miejsca poświęciliśmy liczbom naturalnym. Od nich się wszystko zaczęło. Przez wiele wieków ludzie zajmowali się tylko liczbami naturalnymi. Szczególnie wiele o nich i ich własnościach dowiedzieliśmy się od starożytnych greków. Grecy uważali, że wszystko na świecie co można policzyć, zważyć lub zmierzyć wyraża się w liczbach naturalnych.

Ułamki, liczby wymierne też można opisać jako parę liczb naturalnych. Czy jednak liczby wymierne wyczerpują oś liczbową, czy za ich pomocą można opisać wszystkie zjawiska otaczającego nas świata. Pierwsze wątpliwości wprowadził Pitagoras (VI w. p. n. e.), któremu przypisuje się autorstwo słynnego twierdzenia o bokach w trójkącie prostokątnym. Pomimo, że własności trójkąta prostokątnego już wcześniej stosowano w budownictwie, to dopiero Pitagoras opisał je w formie twierdzenia, które następnie udowodnił.

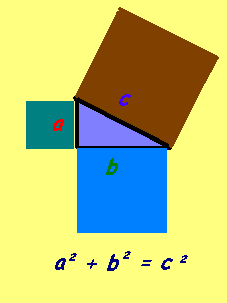
Już starożytni filozofowie wiedzieli o istnieniu różnych trójek liczb (a, b, c) takich, że: a2+b2=c2.

Przedstawienie tej własności liczb w postaci twierdzenia i udowodnienie go, doprowadziło Pitagorasa niesamowitego odkrycia, istnienia liczby, której nie potrafili wyznaczyć. Jeżeli kwadrat ma bok 1, to jego przekątna długość a taką, że a²=2. Widać, że a nie jest liczbą naturalną. Czy a jest liczbą wymierną, to znaczy czy da się przedstawić w postaci a=m/n?
Przypuśćmy, że a=m/n, gdzie m,n są liczbami naturalnymi. Wtedy m²/n²=2, czyli m²=2n². Czy taka równość jest prawdziwa? Sprawdzimy to na przykładzie:
10²=10*10=(2*5)*(2*5)=2*2*5*5,
8²=8*8=(2*2*2)*(2*2*2)=2*2*2*2*2*2,
42²=42*42=(2*3*7)*(2*3*7)=2*2*3*3*7*7.
Łatwo zauważyć, że w m² każdy czynnik występuje parzystą ilość razy, niezależnie od tego jaką liczbę przeanalizujemy. Ale w 2*n² czynnik 2 wystąpi zawsze nieparzystą ilość razy. Nie może więc być równości pomiędzy m² i 2n². Czyli a nie można przedstawić w postaci liczby wymiernej. Powtarzając powyższe rozumowanie można łatwo udowodnić niewymierność a dla a²=3, a²=5, a²=6 i wielu innych liczb. Okazuje się, że na osi liczbowej, poza liczbami wymiernymi znajduje się jeszcze wiele innych liczb, które nie dają się zapisać za pomocą ułamka. Te liczby nazywamy liczbami niewymiernymi. Przekątna i bok kwadratu są odcinkami niewspółmiernymi. Geometrycznie umiemy budować odcinki niewspółmierne. Algorytm postępowania przy ich obliczaniu zostanie umieszczony w zadaniach praktycznych.

Opracowane na podstawie: Liczby i algorytmy, Krystyna Dałek, Wydawnictwa Szkolne i Pedagogiczne Warszawa 1987 rok.